ASA

HL

Congruence with proofs

http://rookery9.aviary.com.s3.amazonaws.com/6442500/6442673_26d1_625x625.jpg

2nd semester 5/6 class had talked about congruence with triangles. Congruence included statemnets with proofs. These prooves are statements that tell wether or not the triangles are equal in certain measurements. The final proofs concluded the triangles congruency. These statments are Side,side,side(sss): proofing all sides are the same. side,angle,side(sas):proofing a side then an angle then side. Angle,angle,side(aas,saa): proofing angle,angle, then a side. Angle,side,angle(asa): An angle then a side then a angle. Last Hypotynuse leg(HL): if the triangles are right the longest side(Hypotynuse).

circle concepts

Angle c is right because if a side on a triangle inside the circle(inscribed triangle) is the diameter the triangle is always a right triangle. 

Some examples of circle concepts:

The straight green lines outside of the circle are tangent lines because they touch exactly one point on the circle, the faint line connecting points of tangency is a chord which is a line connecting any two points in the circle without crossing the diameter.  

angle a and angle b are congruent because they catch the same arc which is the pink part of the circle.

Angle c,b and a are all central angles because they are all in the center of the angle.

Angle a is the inscribed angle which is catches one point anywhere on the circumference of the circle.

line pba is secant because it is a chord that extends outside the cirlce. 

art museum

quadrilaterals

The past few weeks my 5/6 geometry class has been going over quadrilaterals.  A quadrilateral is a 2 dimensional polygon that has 4 straight sides.  The shapes we learned about was a parallelogram(1), rhombus(2), square(3), trapezoid(4), kite(5), rectangle(6).  Each shape has it's special properties but also shares these properties with each other.
(1) The parallelogram has opposite angles congruent, opposite sides are congruent and parallel and diagonals bisect.
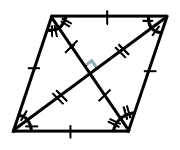 (2) The rhombus's diagonals bisect each other at 90 degrees and all sides are equal.
(3)
        (4) The trapezoid has one pair of opposite sides parallel.


            (5) The diagonals of kite which bisects each other at right angles to form 90 degrees, longer sides of a kite are congruent and the smaller sides of the kite are congruent and the longer diagonal bisects the smaller diagonal. 
        (6) angles measures 90 degrees, opposite sides are parallel, opposite sides are equal, Its diagonals are equal, diagonals bisect each other.